
Αχ αυτό μηδέν!
Στη σειρά του ΒΗΜΑ-Science για όσους θέλουν να φτιάξουν ξανά τη… σχέση τους με τα Μαθηματικά, μπήκαμε στην ενότητα των συστημάτων αρίθμησης και λύνουμε απορίες, ακόμα και σχολικού τύπου!
Spotlight
-

Καθηγητής του Χάρβαρντ: «Απεχθάνομαι το ιρανικό καθεστώς, αλλά έχει δίκιο – Ένοχες οι ΗΠΑ»
-

Κλειστοί δρόμοι στην Αθήνα το Σάββατο για την Ολυμπιακή Φλόγα
-

Η ιστορική φράση του Ανδρέα Παπανδρέου πριν εκλεγεί πρόεδρος του ΠΑΣΟΚ για τελευταία φορά
-
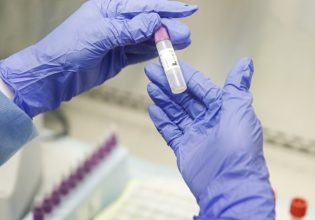
Πέθανε ο μακροβιότερος ασθενής με COVID - Υπέφερε για 613 μέρες και πέρασε 50 μεταλλάξεις
Την προηγούμενη φορά επιβεβαιώσαμε το ότι ένας ακέραιος που υψώνεται στη μηδενική δύναμη θα πρέπει να θεωρούμε ότι ισούται με τη μονάδα, ότι είναι ισοδύναμο το να λες πως υψώνεις έναν πραγματικό αριθμό εις την ½ με το να αναζητήσεις την τετραγωνική του ρίζα, και ακόμη ότι και το 0 εις τη μηδενική δύναμη τείνει προς μια τιμή πολύ κοντά στη μονάδα, άρα συμβατικά θα θεωρούμε πως μπορεί να έχει κάποιο νόημα η ισότητα 0 0 = 1 αρκεί να μένουμε προσεκτικά μέσα στους πραγματικούς αριθμούς (διότι υπάρχει ακριβώς δίπλα και ένα άλλο «δάσος», το πεδίο των φανταστικών ή μιγαδικών αριθμών με κάποιους δικούς του κανόνες, που μας υποχρεώνουν να ασχοληθούμε μαζί του ξεχωριστά).
Το μηδέν είναι υπεύθυνο για κάποιες τέτοιες ιστορίες διότι πρόκειται για ένα περίεργο και άγριο πλάσμα της ανθρώπινης σκέψης, που δεν πρέπει να χάνεις τον έλεγχό του. Ούτε να το προσπερνάς στα γρήγορα, όταν διδάσκεις, σαν να φοβάσαι ότι θα σε δαγκώσει.
«Αγριες» ιστορίες
Μια ιστορία λοιπόν με ήρωα το μηδέν αρχίζει όταν φθάσουμε να σκεπτόμαστε όπως και ο υπολογιστής! Οτι η διαίρεση είναι διαδοχικές αφαιρέσεις. Δηλαδή για να βρούμε το 15/5 μπορούμε να κάνουμε το εξής: 15 – 5 = 10, 10 – 5 = 5, 5 – 5 = 0. Τρεις αφαιρέσεις, άρα 15/5 = 3. Αν όμως είχαμε 15/0; Τι θα κάναμε; Οι αφαιρέσεις 15 – 0 – 0 – 0 – 0… δεν οδηγούν κάπου.
Ας ξεκινήσουμε αλλιώς. Με ό,τι πιο απλό, με το κλάσμα (1/1) = 1. Συνεχίζουμε βάζοντας διαδοχικά ως παρονομαστές τα 0,1, 0,01, 0,001, 0,0001, και παρατηρούμε πως παίρνουμε αντίστοιχα 1, 10, 100, 1.000, 10.000 και αν συνεχίσουμε τα αποτελέσματα τείνουν σε κάτι πολύ μεγάλο όσο ο παρονομαστής πλησιάζει στο μηδέν. Ας το πούμε «άπειρο» αυτό το όριο. Αν όμως πάρουμε και το κλάσμα (2/1) και αρχίσουμε να μικραίνουμε τον παρονομαστή, θα πάρουμε αντίστοιχα 2, 20, 200, 2.000, 20.000, άρα πάλι στο άπειρο θα καταλήξουμε. Αν όμως μπούμε στον πειρασμό να βάλουμε (1/0) = ∞ και (2/0) = ∞, αν και το άπειρο δεν είναι καν αριθμός, θα είμαστε υποχρεωμένοι να εξισώσουμε: (1/0) = (2/0) που δίνει το απαράδεκτο 1 = 2.
Για τον λόγο αυτόν το σωστό είναι όχι να πούμε πως η διαίρεση διά του μηδενός είναι αδύνατη αλλά ότι δεν είναι (καν) προσδιορίσιμη και δεν επιτρέπουμε να εισχωρεί στους υπολογισμούς και στις διερευνήσεις μας. Και αυτό ας μη συγχέεται με μια διαίρεση της μορφής: (0/1) ή (0/2), (0/3) κ.λπ. Ολα αυτά τα κλάσματα είναι ίσα με μηδέν και για να το καταλάβουμε αρκεί απλώς να σκεφθούμε πως το να μοιράσουμε 0 πράγματα σε 1,2 ή 3 ανθρώπους δίνει μηδενικό αποτέλεσμα.
Πνευματική γυμναστική
1. Ενα αγόρι και ένα κορίτσι κάθονται στο παγκάκι ενός πάρκου. Το άτομο που έχει μαύρα μαλλιά λέει: «Είμαι αγόρι». Το άτομο που έχει ξανθά μαλλιά λέει: «Είμαι κορίτσι». Αν είναι σίγουρο ότι τουλάχιστον το ένα από τα δύο άτομα λέει ψέματα, να προσδιοριστεί ποιο είναι το αγόρι και ποιο το κορίτσι.
2. Εχουμε ένα τροποποιημένο τραπέζι του μπιλιάρδου με οπές μόνο στις τέσσερις γωνίες. Ξεκινώντας από τη θέση ακριβώς μπροστά από την κάτω αριστερή οπή, με τη στέκα αναγκάζουμε μια μπάλα να ακολουθήσει ευθύγραμμη τροχιά, σε γωνία 45 μοιρών, ως προς την οριζόντια πλευρά. Αν οι διαστάσεις του τραπεζιού είναι 9 μονάδες για το μήκος και 7 μονάδες για το πλάτος, δεν υπάρχουν τριβές και οι ανακλάσεις της μπάλας είναι τέλειες, θα καταλήξει η μπάλα σε κάποια από τις οπές και αν ναι σε ποια;
Οι λύσεις του προηγούμενου κουίζ
1. Κάποια κοπέλα πήρε δώρο ένα ρολόι που πήγαινε μπροστά 6 λεπτά σε κάθε μία ώρα. Το ρολόι είχε ρυθμιστεί να δείχνει τη σωστή ώρα ακριβώς τα μεσάνυχτα της προηγούμενης ημέρας. Οταν πήρε στα χέρια της αυτό το ρολόι την επόμενη ημέρα έδειχνε 8.26 το πρωί. Αλλά ήδη ήταν σταματημένο 30 λεπτά πριν. Ζητούσαμε να βρεθεί τι ώρα ήταν πραγματικά τη στιγμή που το πήρε στα χέρια της. Μέχρι να σταματήσει δείχνοντας 8.26 π.μ. πέρασαν για το ελαττωματικό ρολόι 506 λεπτά. Πρέπει να βρούμε πόσα πραγματικά λεπτά είχαν περάσει. Ξέρουμε πως για τα 60 πραγματικά λεπτά στο ελαττωματικό ρολόι αντιστοιχούν 60 + 6 = 66 λεπτά. Αρα για τα 506 του ελαττωματικού ρολογιού αντιστοιχούν: (60 Χ 506)/66 = 460 πραγματικά λεπτά. Που αντιστοιχούν σε 7 ώρες και 40 λεπτά. Προσθέτουμε και τα 30 (που θεωρούμε πως ήταν πραγματικά) λεπτά, οπότε φθάνουμε στις 7 ώρες και 70 λεπτά ή 8 ώρες και 10 λεπτά, άρα η ώρα ήταν τελικά 8.10 το πρωί.
2. Είχαμε τον πατέρα που αποφασίζει να μοιράσει μαργαριτάρια στις κόρες του και δίνει στη μεγαλύτερη ένα μαργαριτάρι και ένα έβδομο από τα υπόλοιπα μαργαριτάρια, στη δεύτερη δύο και ένα έβδομο από τα υπόλοιπα, στην τρίτη τρία και το ένα έβδομο των υπολοίπων. Συνεχίζοντας έτσι μέχρι την τελευταία κόρη. Ζητούσαμε να βρεθεί πόσες κόρες είχε, πόσα μαργαριτάρια, και αν αδίκησε κάποια. Ας εξετάσουμε τι έγινε δεχόμενοι ότι όλες πήραν τα ίδια και δεν αδικήθηκε κάποια. Η τελευταία κόρη, ας πούμε η κ στη σειρά, πήρε κ μαργαριτάρια και τίποτα άλλο, αφού δεν θα έπρεπε να έχουν μείνει άλλα (αφού θα ήταν πρόβλημα το ποια θα τα έπαιρνε). Αφού όμως πήραν όλες τον ίδιο αριθμό, θα έχουμε ότι σε καθεμία δόθηκαν κ μαργαριτάρια. Οπότε κ επί κ = κ 2. Για την προηγούμενη, την κ-1, ισχύει ότι πήρε κ-1 και 1/7 αυτών που έμεναν. Αλλά αυτό το 1/7 θα πρέπει να ήταν 1 μαργαριτάρι, για να συμπληρωθεί και το δικό της μερίδιο που έπρεπε να είναι κ. Διότι όντας η (κ-1) στη σειρά έπαιρνε (κ-1) +1 = κ. Αρα πριν πάρει και η κ τα δικά της, έμεναν κ + 1 που έπρεπε στη διαίρεση με το 7 να δίνουν αποτέλεσμα 1. Δηλαδή (κ + 1)/7 = 1, οπότε κ + 1 = 7, άρα το κ είναι ίσο με 6. Και έτσι πήραν από 6 και ήταν 6 κόρες, έγινε δίκαιη μοιρασιά και δεν χρειάζεται να εξετάσουμε άλλη περίπτωση.
Ακολουθήστε το in.gr στο Google News και μάθετε πρώτοι όλες τις ειδήσεις














































 Αριθμός Πιστοποίησης Μ.Η.Τ.232442
Αριθμός Πιστοποίησης Μ.Η.Τ.232442