
Αριθμοί, Τέχνη και Ομορφιά
Στη σειρά του ΒΗΜΑ-Science για όσους θέλουν να φτιάξουν ξανά τη «σχέση» τους με τα Μαθηματικά, για τις ημέρες που έρχονται, επιχειρούμε μια απόδραση από την ακαδημαϊκή γνώση: εξετάζουμε το αν κάποια αισθητική όχι μόνο συγκατοικεί με τα Μαθηματικά, αλλά και το αν διάφορα εικαστικά στοιχεία θα μπορούσαν να συμβάλουν στην εξοικείωσή μας με αυτά
Spotlight
-

Όμηρος της Χαμάς εμφανίζεται σε βίντεο με ακρωτηριασμένο χέρι - «Οι IDF σκότωσαν 70 από εμάς»
-
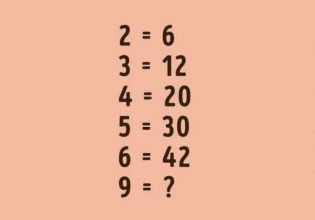
Ποιος αριθμός λείπει; - Βρείτε τη λύση σε 10 δευτερόλεπτα και αποδείξτε πόσο μαθηματικό μυαλό έχετε
-

BBC για την αφρικανική σκόνη: «Η καταχνιά της Σαχάρας έπνιξε την Αθήνα»
-

Η Μάργκοτ Ρόμπι «μιλά» στη νοηματική και γίνεται viral
Οι δύσκολες στιγμές της ανθρωπότητας έχει αποδειχθεί ότι μπορεί να φέρνουν μαζί τους και απροσδόκητες ευκαιρίες για να καθιερωθούν σε μεγάλες περιοχές της Γης και κάποιοι λυτρωτικοί θεσμοί ή να αλλάξει μια μεγάλη μερίδα ανθρώπων τις προηγούμενες συνήθειές της. Η ιδέα του Ερυθρού Σταυρού προέκυψε από τον Ιταλοαυστριακό πόλεμο του 1859. Τα εμβόλια για τη φυματίωση και την πολιομυελίτιδα από τις βαριές συνέπειες και τη μεγάλη εξάπλωση αυτών των ασθενειών, η παγκόσμια εκστρατεία για τη μείωση του καπνίσματος από τη στενή σχέση του με τον καρκίνο.
Η επίμονη και σε παγκόσμια κλίμακα εξάπλωση του κορωνοϊού φαίνεται πως θα αφήσει πίσω της κάποια εμβόλια, αλλά μήπως θα μπορούσε να γίνει και αιτία ώσμωσης μεταξύ πραγμάτων που μέχρι τώρα υπήρχαν αμφιβολίες για τη μεταξύ τους συμβατότητα;
Για παράδειγμα, είδαμε ότι από τον Φεβρουάριο η πανδημία επέβαλε τηλεργασία και τηλεκπαίδευση. Πριν καν υπάρξει υποψία για το ότι θα μπορούσε μια μολυσματική ασθένεια να κλείσει τα σχολεία και τους μαθητές στα σπίτια τους είχε προβληματίσει αρκετά, σε χώρες της Βόρειας Ευρώπης κυρίως, το αν και πώς θα μπορούσε να ενσωματωθεί η τεράστια εργαλειοθήκη που προσφέρεται μέσα από το Διαδίκτυο. Για εμπλουτισμό αλλά ίσως και καθολική αλλαγή της σχολικής διδασκαλίας στον τομέα της απόκτησης γνώσεων από τους μικρούς και τους μεγάλους μαθητές. Τώρα αυτό το θέμα μάς πλησίασε όλους με ταχύτητα χιονοστιβάδας και μας πονάει. Γιατί μας βρίσκει χωρίς ιδιαίτερα πρωτότυπες ιδέες και τα παιδιά να πλήττουν μπροστά σε άγονες οθόνες χειρότερα από ό,τι έπλητταν μέσα στην τάξη.
Κάτω από τα δάχτυλα βρίσκονται αναρίθμητες ευκαιρίες για την απόκτηση γνώσεων, αλλά πρέπει όχι μόνον να ξέρεις να πατήσεις τα κατάλληλα πλήκτρα αλλά κάποιος να σου έχει δημιουργήσει αρχικά τη διάθεση για αυτό και τελικά να σε έχει πείσει κιόλας. Και τα δώδεκα χρόνια επαφής υποχρεωτικής με το σχολικό περιβάλλον, όπως έχει θεσπιστεί (που για κάποιους γίνεται αισθητή και ως καταναγκασμός), αντιστοιχώντας σε χιλιάδες ώρες προγραμματισμένων ενεργειών, θα ήταν υπεραρκετά για να βγαίνεις στον κόσμο ακέραιος αλλά και γεμάτος αισιοδοξία.
Ζωγραφική και Γεωμετρία
Μεταξύ αυτών φυσικά και οι ώρες διδασκαλίας των Μαθηματικών. Σίγουρα ένα κομμάτι της εκπαίδευσης που μπορεί να αφήσει άσχημες αναμνήσεις σε κάποιους μαθητές και κάποιες μαθήτριες. Αν όμως αυτοί που είναι υπεύθυνοι για τη διαμόρφωση «της ύλης και των προγραμμάτων» δέχονταν κατ’ αρχάς τα αισθητικά στοιχεία που συγκατοικούν με τις μαθηματικές δομές και κατέβαζαν στη συνέχεια καμιά πιο ρηξικέλευθη ιδέα για το πώς αυτό θα φανερωνόταν στο σχολικό περιβάλλον; Αν για παράδειγμα συνεργαζόταν στενά αυτός που διδάσκει τα έως σήμερα συμβατικά Μαθηματικά με αυτόν που διδάσκει Ζωγραφική (και Μουσική προφανώς); Αν ζωγράφιζαν τα παιδιά την ώρα των Μαθηματικών και συζητούσαν για Γεωμετρία την ώρα των καλλιτεχνικών;
Φεύγουμε για μια στιγμή από το σχολικό περιβάλλον για να ρίξουμε μια ματιά σε εργασία που δημοσιεύθηκε τον Φεβρουάριο του 2014 και είχε τίτλο: «Η εμπειρία της ομορφιάς των Μαθηματικών και η νευρωνική σχέση» (https://www.frontiersin.org/articles/10.3389/fnhum.2014.00068/full#F1).
Σε 15 μαθηματικούς (3 γυναίκες, 12 άνδρες) δόθηκαν 60 μαθηματικές παραστάσεις να τις μελετήσουν με την ησυχία τους και να τις κατατάξουν κατά την άποψή τους σε όμορφες, αδιάφορες και άσχημες (σε κλίμακα από το -5 έως το +5). Στη συνέχεια κάποια στιγμή τους κάλεσαν στο εργαστήριο και άρχισαν να τις προβάλλουν στον καθένα έχοντας συνδέσει ηλεκτρόδια σε μια περιοχή του προμετωπιαίου φλοιού η οποία εμπλέκεται στη γνωσιακή διαδικασία λήψης αποφάσεων. Μέτρησαν την αντίδρασή τους και αποδείχθηκε ότι οι παραστάσεις που θεωρήθηκαν ως «όμορφες» προκαλούσαν διέγερση σε αυτή την περιοχή ακριβώς όπως και άλλες πηγές, άσχετες με αριθμούς και εξισώσεις, που εξ ορισμού αυτές θεωρείται ότι σχετίζονται με κάτι όμορφο.
Πρωταθλήτρια αναδείχθηκε η εξίσωση του Οϊλερ: 1 + e iπ = 0 και κοντά της το Πυθαγόρειο Θεώρημα. Το ουσιαστικό όμως είναι πως για τα Μαθηματικά υπάρχει ένας χώρος που μπορούν να συμπλέκονται γόνιμα Τέχνη, εξισώσεις, αποδείξεις, αριθμοί. Ετσι, όσοι έχουν μια καλή σχέση με αυτά, νιώθουν τα ίδια συναισθήματα που τους διακατέχουν και όταν αντικρίζουν ένα γλυπτό ή έναν πίνακα.
Πνευματική Γυμναστική
- Ας δούμε, λόγω των ημερών, ένα πρόβλημα που μας έρχεται από την Ανατολή. Αποδίδεται στον Ali-Ibn-Abi-Talib, τον τέταρτο χαλίφη του Ισλάμ (600-661 μ.Χ.): Υποθέτουμε ότι στο ταξίδι τους προς τη Μεσόγειο τρεις άνθρωποι σταμάτησαν κάπου για να γευματίσουν. Ο πρώτος είχε προμηθευτεί φεύγοντας 5 φραντζόλες ψωμί και ο δεύτερος 3 φραντζόλες. Ο τρίτος, ο Αλή, κάθισε μαζί τους και μοιράστηκαν οι τρεις τους σαν ίσοι το ψωμί. Στο τέλος ο Αλή βγάζει και δίνει 8 ίδιας αξίας νομίσματα για να ευχαριστήσει τους άλλους δύο. Ο πρώτος λέει τότε πως πρέπει να πάρει 5 νομίσματα και τα υπόλοιπα ο δεύτερος. Εκείνος όμως είχε αντίρρηση και ισχυρίστηκε πως το σωστό ήταν να πάρουν από 4. Τότε επενέβη ο Αλή και είπε στον δεύτερο ότι δεν τον συμφέρει που κάνει φασαρία διότι κανονικά έπρεπε να πάρει μόνο 1 και ο πρώτος 7. Ηταν σωστό αυτό που τους είπε ο Αλή;
- Γιατί είναι σίγουρο πως αν ψάξουμε σε ολόκληρο τον κόσμο, θα υπάρχουν τουλάχιστον δύο άνθρωποι που αν μετρήσουμε τις τρίχες στα κεφάλια τους θα τις βρούμε ακριβώς ίσες σε αριθμό;
Οι λύσεις των προηγουμένων κουίζ
- Zητούσαμε να βρεθεί ο αριθμός που το τελευταίο του ψηφίο δεξιά είναι 4 και όταν αυτό το 4 το πάρουμε από εκεί και το τοποθετήσουμε ως πρώτο ψηφίο αριστερά, ο νέος αριθμός είναι τέσσερις φορές μεγαλύτερος από τον προηγούμενο. Εξαιτίας αυτού του τελευταίου εξετάζουμε το αποτέλεσμα με τον πολλαπλασιασμό με το 4. Ξεκινάμε από το τελευταίο ψηφίο του ζητούμενου αριθμού και παρατηρούμε τι γίνεται αν αρχίσουμε να κάνουμε πολλαπλασιασμό με το 4. Εχουμε 4 x 4 = 16, άρα το προτελευταίο ψηφίο θα είναι το 6 και θα έχουμε το 1 ως κρατούμενο. Συνεχίζουμε κάνοντας το ίδιο: 4 x 6 = 24 + 1 = 25. Στη συνέχεια 4 x 5 = 20. Συν 2 το κρατούμενο = 22. Κρατάμε το 2 και το 2 ως κρατούμενο. 4 x 2 = 8 συν 2 = 10. Κρατάμε το 0 και έχουνε το 1 ως κρατούμενο. Τέλος 4 x 0 = 0 συν 1 = 1. Αρα ο αριθμός είναι: 102.564.
- Ρίχνοντας ένα ζάρι και αθροίζοντας τα αποτελέσματα, μέχρι να πάρουμε άθροισμα μεγαλύτερο από το 12, ζητούμε να προσδιοριστεί εκείνο το άθροισμα που έχει τις περισσότερες πιθανότητες να προκύψει αν επαναλάβουμε πολλές-πολλές φορές τη διαδικασία. Τα αθροίσματα που θα βγάλουμε από τις διαδοχικές ζαριές θα είναι από 13 έως και 18. Υπάρχουν περισσότεροι συνδυασμοί για να φτάσει κάποιος στο 13 από ό,τι στα άλλα αθροίσματα (από 14 έως 18), διότι εκτός των άλλων υπάρχει η περίπτωση να είμαστε στο 12 και να φέρουμε στην επόμενη ζαριά 1. Επομένως, αν επαναλάβουμε αυτή τη διαδικασία 1.000 φορές με ένα «τίμιο» ζάρι, το 13 θα πρέπει να βγει πιο πολλές φορές. Προσοχή όμως. Στην ίδια αυτή διαδικασία θεωρητικά θα βγει πιο πολλές φορές κάποιο από τα αθροίσματα 14-18 αφού αυτά ως προς το πλήθος είναι περισσότερα.
Ακολουθήστε το in.gr στο Google News και μάθετε πρώτοι όλες τις ειδήσεις










































 Αριθμός Πιστοποίησης Μ.Η.Τ.232442
Αριθμός Πιστοποίησης Μ.Η.Τ.232442